In this lecture:
- Just a refresher on some select things we've gone through.
- Some random questions that will hopefully refresh you momeory on the more important concepts
Deep Neural Networks¶
Look at the following 2-layer network:
class TwoLayerModel(nn.Module):
def __init__(self, N, L, M):
super().__init__()
self.N = N # input dimension
self.M = M # number of classes
self.weight_matrix1 = nn.Linear(N, L, bias=True) # N input dimensions, L hidden dimensions
self.weight_matrix2 = nn.Linear(L, M)
def forward(self, x):
x = self.weight_matrix1(x)
z = self.weight_matrix2(x)
return z
--------------------------------------------------------------------------- NameError Traceback (most recent call last) Cell In[1], line 1 ----> 1 class TwoLayerModel(nn.Module): 2 def __init__(self, N, L, M): 3 super().__init__() NameError: name 'nn' is not defined
There something wrong with it....what?
class TwoLayerModel(nn.Module):
def __init__(self, N, L, M):
super().__init__()
self.N = N # input dimension
self.M = M # number of classes
self.weight_matrix1 = nn.Linear(N, L, bias=True) # N input dimensions, L hidden dimensions
self.weight_matrix2 = nn.Linear(L, M)
def forward(self, x):
x = self.weight_matrix1(x)
x = torch.nn.functional.relu(x)
z = self.weight_matrix2(x)
return z
We know that floats have a specific format in computing:
 (pic from [wikipedia](https://en.wikipedia.org/wiki/Single-precision_floating-point_format))
(pic from [wikipedia](https://en.wikipedia.org/wiki/Single-precision_floating-point_format))
Where the real value assumed by this series of 1/0's is:
$$ -1^{b32} \cdot 2^{exponent} \cdot 1.\left\{fraction\right\} $$This is not a continuous space!
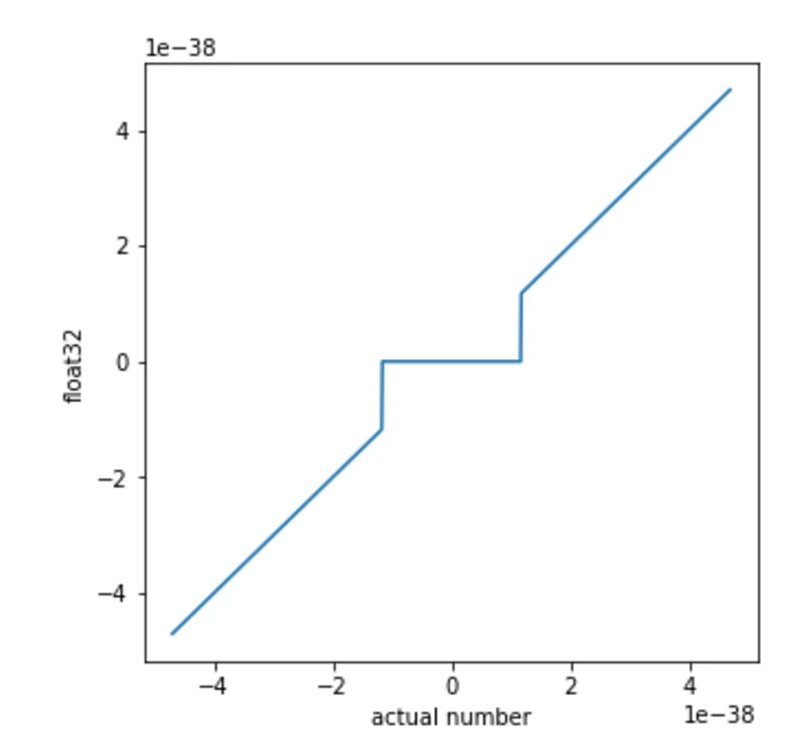
There is a minimum "step" where (for instance) $(a+b)\cdot c$ is not equal to $a \cdot c + b \cdot c$
At the smallest scale, addition becomes non-linear.
We wanted to know if this inherent nonlinearity could be exploited as a computational nonlinearity, as this would let deep linear networks perform nonlinear computations. The challenge is that modern differentiation libraries are blind to these nonlinearities at the smallest scale. As such, it would be difficult or impossible to train a neural network to exploit them via backpropagation.
We can use evolution strategies (ES)(opens in a new window) to estimate gradients without having to rely on symbolic differentiation. Using ES we can indeed exploit the near-zero behavior of float32 as a computational nonlinearity. When trained on MNIST a deep linear network trained via backpropagation achieves a training accuracy of 94% and a testing accuracy of 92%. In contrast, the same linear network can achieve >99% training and 96.7% test accuracy when trained with ES and ensuring that the activations are sufficiently small to be in the nonlinear range of float32. This increase in training performance is due to ES exploiting the nonlinearities in the float32 representation. These powerful nonlinearities allow any layer to generate novel features which are nonlinear combinations of lower level features.
Layer outputs¶
Problem: You are given the following 2D input matrix (image):
$$ \text{Input} = \begin{bmatrix} 1 & 2 & 0 & 3 \\ 4 & 5 & 6 & 7 \\ 0 & 8 & 9 & 2 \\ 1 & 3 & 5 & 6 \end{bmatrix} $$A convolutional layer is applied with the following properties: • Kernel (filter):
$$ \text{Kernel} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} $$- Stride: 1
- Padding: 0 (“valid” convolution, no padding)
- No bias
- No activation function (linear)
Poblems:
- What is the size of the output matrix?
- Compute the resulting output matrix after applying the convolution.
Problem: You are given the following 2D input matrix (image):
$$ \text{Input} = \begin{bmatrix} 1 & 2 & 0 & 3 \\ 4 & 5 & 6 & 7 \\ 0 & 8 & 9 & 2 \\ 1 & 3 & 5 & 6 \end{bmatrix} $$A pooling layer is applied with the following properties:
torch.nn.MaxPool2d((2,1), stride=(2,1), padding=0)
What is the output?
Parameter estimation:¶
Sample Question: Estimating the Number of Parameters¶
Problem:
You are given a network with the following architecture:
- Input: a 3-channel image of size $4 \times 4$ (i.e., shape $(3, 4, 4)$).
- Layer 1: Batch Normalization layer (applied across the channels).
- Layer 2: Convolutional Layer:
- Number of output channels: 6
- Kernel size: $3 \times 3$
- Stride: 1
- Padding: 0
- No bias term
- Layer 3: Max Pooling Layer:
- Kernel size: $2 \times 2$
- Stride: 2
- Layer 4: Fully Connected (Linear) Layer:
- Takes the flattened output from previous layers.
- Outputs 10 units (e.g., class scores).
Tasks:¶
- For each layer, determine the number of learnable parameters.
- Determine the total number of parameters in the entire network.
import torch
import torch.nn as nn
class SampleNet(nn.Module):
def __init__(self):
super(SampleNet, self).__init__()
self.batch_norm = nn.BatchNorm2d(num_features=3) # 3 input channels
self.conv = nn.Conv2d(
in_channels=3,
out_channels=6,
kernel_size=3,
stride=1,
padding=0,
bias=False
)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.fc = nn.Linear(6 * 1 * 1, 10) # After conv+pool output size is (6, 1, 1)
def forward(self, x):
x = self.batch_norm(x)
x = self.conv(x)
x = self.pool(x)
x = torch.flatten(x, 1) # flatten all dimensions except batch
x = self.fc(x)
return x
# Create model instance
model = SampleNet()
# Function to count the number of parameters
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f"Total number of parameters: {count_parameters(model)}")
Total number of parameters: 238
Solution Outline¶
Step 1: Batch Normalization Layer¶
BatchNorm for convolutional layers usually has 2 parameters per channel:
- 1 learnable scale ($\gamma$)
- 1 learnable shift ($\beta$)
Since input has 3 channels:
$$ \text{BatchNorm parameters} = 2 \times 3 = 6 $$✅ 6 parameters
Step 2: Convolutional Layer¶
Each output channel has a kernel for each input channel.
Thus, for 6 output channels:
Given:
- kernel size: $3 \times 3$
- input channels = 3
- output channels = 6
- No bias
Thus:
$$ \text{Convolutional parameters} = 3 \times 3 \times 3 \times 6 = 162 $$✅ 162 parameters
Step 3: Max Pooling Layer¶
Max pooling has no parameters.
✅ 0 parameters
Step 4: Linear Layer¶
First, find the output size before the Linear layer:
After convolution:
- Output spatial size:
So each output channel has a $2 \times 2$ matrix.
After max pooling ($2 \times 2$ with stride 2):
- $2 \to 1$
Thus, after max pooling:
- Each of the 6 output channels has size $1 \times 1$.
Therefore, flattened input size for the linear layer:
$$ \text{Input size to linear} = 6 \times 1 \times 1 = 6 $$The linear layer maps 6 inputs $\to$ 10 outputs.
Thus:
$$ \text{Linear parameters} = 6 \times 10 + 10 = 70 $$(Weight + bias).
✅ 70 parameters
📈 Final Summary:¶
| Layer | Parameters |
|---|---|
| BatchNorm | 6 |
| Convolution | 162 |
| Max Pool | 0 |
| Linear (Fully Connected) | 70 |
Total number of parameters:¶
$$ 6 + 162 + 0 + 70 = 238 $$✅ 238 parameters
✨ Additional Notes:¶
You can make it harder by:
- Using padding=1 in convolution (would change dimensions).
- Adding bias to convolution.
- Having multiple linear layers.
- Making BatchNorm affine=False (no learnable parameters).
- Using different strides in pooling/convolution.
Network shaping¶
In this problem, you will be hand designing a simple neural network to model a specific function. Assume $x \in \mathbb{R}$ and provide appropriate weights $w_0, w_1 \in \mathbb{R}^2$. In other words, the neural network has one input neuron, 2 hidden neurons, and one output neuron.
Find $w_0, w_1 \in \mathbb{R}^2$ such that
$$f(x) = w_1^T \sigma(w_0 x + a) = x+5, \ \forall x \in \mathbb{R}$$where $\sigma = \text{ReLU}$ (note: $w_0 x$ here is a vector-scalar product: $\mathbb{R}^2 \times \mathbb{R} \rightarrow \mathbb{R}^2$, e.g. $[0, 1]^T x = [0, x]^T$). Show why your answer is correct.
In order to achieve this function, we can set $w_0 = [1, -1]^T, w_1 = [1, -1]^T, a = [5, -5]^T$. We can see that this works because applying our answer to our function, we get
$$\begin{align*}\begin{gathered}f(x) = w_1^T \sigma(w_0x + a) = [1, -1]^{T^T}\sigma([1, -1]^Tx + [5, -5]^T) = [1, -1]\sigma([x + 5, -x - 5]^T) \\= [1, -1]\sigma([x + 5, -(x + 5)]^T) = \begin{cases} [1, -1][x + 5, 0]^T = x + 5 &, x + 5 > 0 \\ [1, -1][0, 0]^T = 0 &, x + 5 = 0 \\ [1, -1][0, -x - 5]^T = x + 5 &, x + 5 < 0 \\ \end{cases} \\ \Rightarrow f(x) = x + 5, \forall x \in \mathbb{R}\end{gathered}\end{align*}$$(ReLU: $\sigma(x) = max(0, x)$).
Transformers¶
Some rapid fire questions:
- What are the three types of attention in the standard transformers architecture?
- Besides missing the encoder, what is the difference between the standard transformers model and decoder-only trasnformer model?
- What task(s) are encoder-only transformer model good for?
- What task(s) is a decoder only transformer model good for?
That's it for today¶
- Good luck on the exam Thursday
- Make sure you keep pluggin away on the final projects
- See you next week
References¶
[1] OpenAI "Nonlinear computation in deep linear networks" - https://openai.com/index/nonlinear-computation-in-deep-linear-networks/
